Midpoint Circle Drawing Algorithm in Computer Graphics

Midpoint Circle Cartoon Algorithm in Computer Graphics

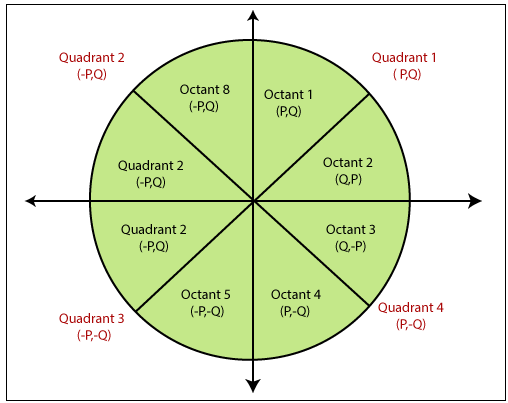
The midpoint circumvolve drawing algorithm helps u.s.a. to calculate the complete perimeter points of a circle for the starting time octant. Nosotros can quickly find and calculate the points of other octants with the help of the first octant points. The remaining points are the mirror reflection of the first octant points.

This algorithm is used in computer graphics to define the coordinates needed for rasterizing the circle. The midpoint circle drawing algorithm helps united states to perform the generalization of conic sections. Bresenham's circle drawing algorithm is likewise extracted from the midpoint circle drawing algorithm. In the algorithm, we will apply the 8-fashion symmetry holding.

In this algorithm, we ascertain the unit interval and consider the nearest bespeak of the circumvolve boundary in each stride.

Allow united states assume we have a point a (p, q) on the purlieus of the circle and with r radius satisfying the equation f_c (p, q) = 0

As we know the equation of the circle is –

f_c (p, q) = pⁱⁱ + qⁱⁱ = r²     …………………………… (i)

If

f_c (p, q) < 0

then

The point is inside the circumvolve purlieus.

If

f_c (p, q) = 0

then

 The bespeak is on the circle boundary.

If

f_c (p, q) > 0

then

 The point is outside the circumvolve purlieus.

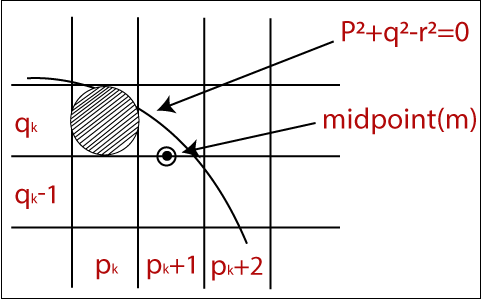
In the figure, nosotros calculate the mid-point (chiliad). The midpoint appears between q_thousand and q_yard -1.

The currentposition of the pixel = p_k +one

The next position of the pixel = (p_yard +i, q_g) and (p_g +1, q_k - ane)

At present, we will summate the decision parameter (d_grand)

d_k = (p_thousand +1, q_{one thousand} – 1/two)

Now, we replace all the values with equation (1)

d_k = (p_m +1)ⁱⁱ + (q_k – one/two)ⁱⁱ – r^{two                          ……………………………………} (ii)

Now, there should be two conditions.

Status 1: If

d_{one thousand} is negative

and so

The midpoint (m) is within the circumvolve boundary

Condition 2: If

d_k is positive

and so

The midpoint (m) is outside the circle boundary

Now, we find the next indicate of x coordinates. Then,

P_k+i +1 = P_chiliad+ii

At present, nosotros replace all the value of equation (2) with (m+1). We get-

d_k+ane = (p_grand+one +ane)² + (q_k+ane – 1/2)² – r^two                ……………………………. (3)

Now, nosotros volition notice the difference between

d_k+1 – d_k = {(p_thousand+ane +1)^two + (q_k+1 – 1/2)² – r²} – {(p_k +1)² + (q_k – one/ii)² – r²}

               = d_thou +(2p_k +1) + (q_g+one ^two – q_k ²) – (q_m+1 – q_k) +i    …………………… (4)

Here, If

d_k isnegativethen d_k+1

 then

2p_k+ane +ane

Otherwise

2p_k+one +1 – 2q_chiliad+1

Now, the next coordinate for 10 and y points

2p_k+ane = 2p_k +two

2q_k+1 = 2q_{one thousand} –2

At present, the initial determination parameter (d₀) at the position (p, q) = (0, r)

We put (0, r) in circle equation and we get-

d₀ = (ane, r – 1/2)

    = (1 + (r –1/2)² –r²)

    = 5/4 –r

We only take integer value = i – r

Algorithm of Midpoint Circle Drawing

Step 1: First.

Stride 2: Showtime, we allot the center coordinates (p₀, q­₀) as follows-

P₀ = 0

             q₀ =r

Step 3: At present, nosotros calculate the initial conclusion parameter d₀ -

d₀ = one – r

Stride iv: Presume,the starting coordinates = (p_{one thousand}, q_grand)

The next coordinates will exist (p_k+1, q_k+one)

At present, we discover the side by side point of the first octant according to the value of the decision parameter (d_k).

Step v: Now, nosotros follow two cases-

Case one: If

d_{one thousand} < 0

then

p_k+ane =p_k + 1

                  q_chiliad+1 =q_thou

                  d_k+1 = d_grand + 2 p_chiliad+1 + one

Case 2: If

d_chiliad >= 0

and then

p_k+ane =p_k + one

                  q_yard+1 =q_k –1

                  d_thousand+1 = d_chiliad - two (q_g+ane + two p₁₀₀₀₊₁)+ ane

Step 6: If the center coordinate point (p₀, q₀) is not at the origin (0, 0) then nosotros will draw the points as follow-

For x coordinate = x_c + p₀

For y coordinate = y_c + q₀               {x_c andy_c containsthe electric current value of ten and y coordinate}

Step vii: Nosotros repeat step 5 and 6 until we get x>=y.

Footstep 8: Stop.

Example: The center coordinates are (0, 0), and the radius of the circle is 10. Find all points of the circle by using the midpoint circle drawing algorithm?

Solution:

Footstep one : The given center coordinates of the circle (p_0, q₀) = (0, 0)

Radius of the circumvolve (r) = 10

Step ii: Now, we will determine the starting coordinates (p_0, q₀) as follows-

P₀ = 0

             q₀ = r (radius) = 10

Step three: Now, we will determine the initial decision parameter (d₀)

d₀ = 1 –r

                    d₀ = i –x

                    d₀ = -9

Step 4: The initial parameter d₀ < 0 and then, example 1 is satisfied.

           p_k+1 =p_k + 1 = 0 + 1 = one

                  q_{one thousand+1} =q_k = ten

                  d_k+1 = d_k + 2 p_{one thousand+ane} + 1 = -9 + ii(one) + 1 = -half-dozen

Step v: The center coordinates of circle are already (0, 0). So, motion to next step.

Pace vi: We will execute step 4 until nosotros get x >= y.

The table for coordinates of octant 1-

dk	dg+1	(pk+1,qone thousand+ane)
		(0, 10)
­-ix	-6	(1, 10)
-6	-i	(2, 10)
-i	half-dozen	(3, 10)
6	-3	(4, 9)
-3	viii	(v, 9)
8	v	(half dozen, viii)

Now, we will determine the coordinates of the octant ii by swapping the p and q coordinates.

Points of Octant 1	Points of Octant ii
(0, 10)	(eight, half-dozen)
(1, ten)	(9, 5)
(two, ten)	(nine, 4)
(3, 10)	(10, 3)
(4, 9)	(x, 2)
(5, 9)	(10, 1)
(6, 8)	(10, 0)

Thus, we tin can discover all the coordinates of the circle for all quadrants.

Quadrant 1 (p, q)	Quadrant ii (-p, q)	Quadrant 3 (-p, -q)	Quadrant 4 (p, -q)
(0, 10)	(0, 10)	(0, -10)	(0, -x)
(1, 10)	(-1, 10)	(-1, -ten)	(1, -ten)
(2, ten)	(-2, 10)	(-2, -10)	(2, -x)
(3, x)	(-3, 10)	(-3, -10)	(3, -10)
(4, ix)	(-four, 9)	(-4, -ix)	(four, -nine)
(5, 9)	(-5, 9)	(-5, -nine)	(5, -9)
(6, 8)	(-6, 8)	(-half dozen, -viii)	(6, -viii)
(eight, 6)	(-eight, vi)	(-eight, -6)	(8, -vi)
(9, 5)	(-9, 5)	(-9, -v)	(9, -five)
(9, iv)	(-9, 4)	(-9, -4)	(9, -4)
(x, 3)	(-ten, 3)	(-10, -three)	(ten, -3)
(x, two)	(-10, ii)	(-10, -2)	(10, -two)
(10, 1)	(-x, one)	(-10, -1)	(x, -1)
(10, 0)	(-10, 0)	(-ten, 0)	(x, 0)

Advantages of Midpoint circumvolve cartoon algorithm

• It is a powerful and efficient algorithm.
• The midpoint circumvolve drawing algorithm is easy to implement.
• It is besides an algorithm based on a uncomplicated circle equation (x² + yⁱⁱ = r²).
• This algorithm helps to create curves on a raster display.

 Disadvantages of Midpoint circle drawing algorithm

• It is a time-consuming algorithm.
• Sometimes the points of the circumvolve are not authentic.

• Scan Conversion of an Ellipse Computer Graphics
• Scan Conversion of a Circle Calculator Graphics
• Bresenham's Circle Cartoon Algorithm in Computer Graphics
• Line Cartoon Algorithm in Computer Graphics
• DDA line Drawing Algorithm in Computer Graphics
• 3D Rotation in Computer Graphics
• 2D Rotation in Computer Graphics
• Figurer Graphics Tutorial
• Projection in Computer Graphics
• Animation in Computer Graphics

pruittspecculp1971.blogspot.com

Source: https://www.tutorialandexample.com/midpoint-circle-drawing-algorithm

Share this post